Inverse Variation With Exponents
Inverse Variation With Exponents
Inverse Variation:
Two terms are said to be in inverse variation if increase or decrease of term will result in the decrease or increase of the other term respectively.
For example:let us consider the equation
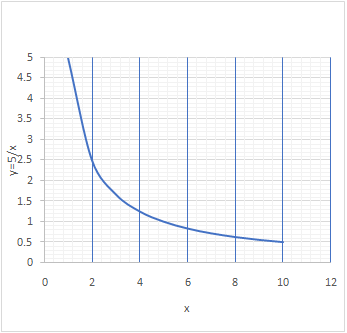
Now let us calculate the value of y for different values of the x
|
x |
1 | 2 | 3 | 4 | 5 |
|
y |
5 | 2.5 | 1.66 | 1.25 | 1 |
If we graph y against x we get the graph below
Inverse Variation With Exponents:
Two terms are said to be in inverse variation with exponents if increase or decrease of term will result in the exponential decrease or increase of the other term respectively.
For example:let us consider the equation
Now let us calculate the value of y for different values of the . Here we include in the table a row for the values of
:
|
x |
1 | 2 | 3 | 4 | 5 |
| 1 | 4 | 9 | 16 | 25 | |
| y | 5 | 1.25 | 0.56 | 0.31 | 0.20 |
If we plot the value y against x we get the graph below. From the graph we can infer that there is an steep fall in the value of y when the value of x increases
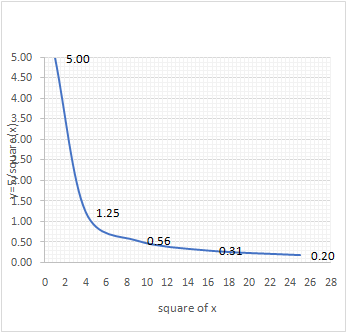
Illustration: Suppose y is inversely proportional to the square of the x , and that y =36 when x = 5
(a) find y when x = 15 (b) given , find x when y = 49 .
Solution: According to the question it is given that
(a) It is given that when x= 5 the value of y = 36 . To find the value of y when x = 15
| x | 5 | 15 |
| y | 36 | ? |
we see that the new value of x is obtained when x is multiplied by 3
(b) It is given that when x= 5 the value of y = 36 . To find the value of y when x = 15
| x | 5 | ? |
| y | 36 | 49 |
we see that the new value of y is obtained when present value of y is multiplied by 49 and divided by 36
From the following equation, state which variables are in inverse relation and find the proportionality constant. | |||
| Right Option : B | |||
| View Explanation | |||
Inverse variation can be written as | |||
| Right Option : C | |||
| View Explanation | |||
Suppose y is inversely proportional to the square of the x , and that y =36 when x = 5 ? Find y when x = 15 | |||
| Right Option : A | |||
| View Explanation | |||
Students / Parents Reviews [10]
It has a great methodology. Students here can get analysis to their test quickly.We can learn easily through PPTs and the testing methods are good. We know that where we have to practice
Barkha Arora
10thMy experience with Abhyas is very good. I have learnt many things here like vedic maths and reasoning also. Teachers here first take our doubts and then there are assignments to verify our weak points.
Shivam Rana
7thA marvelous experience with Abhyas. I am glad to share that my ward has achieved more than enough at the Ambala ABHYAS centre. Years have passed on and more and more he has gained. May the centre flourish and develop day by day by the grace of God.
Archit Segal
7thAbhyas is a complete education Institute. Here extreme care is taken by teacher with the help of regular exam. Extra classes also conducted by the institute, if the student is weak.
Om Umang
10thMy experience with Abhyas academy is very good. I did not think that my every subject coming here will be so strong. The main thing is that the online tests had made me learn here more things.
Hiya Gupta
8thBeing a parent, I saw my daughter improvement in her studies by seeing a good result in all day to day compititive exam TMO, NSO, IEO etc and as well as studies. I have got a fruitful result from my daughter.
Prisha Gupta
8thAbhyas Methodology is very good. It is based on according to student and each child manages accordingly to its properly. Methodology has improved the abilities of students to shine them in future.
Manish Kumar
10thI have spent a wonderful time in Abhyas academy. It has made my reasoning more apt, English more stronger and Maths an interesting subject for me. It has given me a habbit of self studying
Yatharthi Sharma
10thAbout Abhyas metholodology the teachers are very nice and hardworking toward students.The Centre Head Mrs Anu Sethi is also a brilliant teacher.Abhyas has taught me how to overcome problems and has always taken my doubts and suppoeted me.
Shreya Shrivastava
8thIt was good as the experience because as we had come here we had been improved in a such envirnment created here.Extra is taught which is beneficial for future.
